あるデジイチ初心者の記録(v2.0)

某氏から、”Digital Century Puzzle”を解くコードを書けという冬休みの宿題をいただいてしまった。この名前でぐぐってもあまり引っかからないけど、順に並んだ1-9の数字に四則演算とかっこを適用して指定した数になるようにしろという問題。

某氏からはほどほどのところでよいという指示だったのだが、やり始めてみたらいろいろ奥の深い部分もあり、速度に満足いかなくてあれこれ高速化してみたくなったりと、結局かなりの手間をかけたものになってしまった。一応のでき上がりといえるコードはgithubに公開してある。これを拾ってきて、たとえば

  % python digital_century.py 2016

とすると、結果が2016になる式の一覧が表示される。

以下は、実装についてのちょっとした説明と、やってみて気がついたことのメモ。

実装はおもに3つの部分からできている。

最初の部分では、与えられた数字列と四則演算からなる式についての、すべての可能な逆ポーランド記法(Reverse Polish Notation, RPN: wikipedia)の「雛形」を求めている。ここで、RPNの「雛形」とは、通常のRPNで演算子が入る部分を、その部分で連続する演算子の個数で置き換えたもの(注: 専門用語ではなくここでの説明のために用意した独自概念)。たとえば”(1 + (2 + 3)) + 4″を表すRPN”1 2 3 + + 4 +”に対応する「雛形」は”1 2 3 <2> 4 <1>“(“<n>”はこの部分にn個の演算子が入ることを意味する)。9つの数字の場合、このような雛形は全部で1430ある。

2番目の部分では、それぞれの雛形について、演算子部分のスペースに全演算子の組み合わせを適用し、その雛形についてのあり得るすべてのRPNを求め、その値を計算する。ちなみに、9つの数字の場合は演算子は8個になるので、組み合わせの数は4**8=65536個になる。雛形が1430個あるので、結局、1430 * 65536 = 9371万6480個の式を計算することになり、かなりのチカラ技である。

計算結果が目的とする値(“2016″など)と一致する場合は最後の部分に進む。ここでは、まず、そのRPNを普通の数式に変換する。その際、必要な場合に限ってかっこをつける。たとえば上に挙げた例や、”1 2 3 * +”というRPN(= 1 + 2 * 3)ではかっこはまったく含まれない。一方、”1 2 3 + *”の場合は”1 * (2 + 3)”のようにかっこが必要になる。さらに、’-‘や’/’の後にかっこが必要になり得る場合、それを展開してかっこを省けるならそうする。たとえば、”1 – (2 + 3)”は”1 – 2 – 3″に、”1 / (2 * 3)”は”1 / 2 / 3″に展開される(同じ強さの演算子が並んでいる場合は左結合を採用すると仮定している)。この結果、RPNとしては違っていても実質的に同じ式になるものは同じ文字列に変換されるので、重複した式は除いてこれらの式を記録する。

最後に、記録されたすべての式を出力して完了である。

…と、さらっと書いているが、実際には一筋縄ではいかなかった。(速度を別とすると)2番目の部分までは割とすぐにできたのだが、3番目でかなり手間取ってしまった。検算用のreferenceとして、某氏からは以下の二つのblogを紹介されていた

• 「1 2 3 4 5 6 7 8 * * – – / / 9 * * = 2010」
• 「2010」(毎年「今年の式」をつぶやいている某先生のblog)

のだが、これらで使っている”2010″の場合の結果と、最初にさくっとできた(つもりの)実装の出力を比較すると、個数からして一致しない。どこがどう違っているのかを差分を取って詳しく調べてみて、最初に書いた自分の実装では、上に述べた「展開によるかっこの省略」をしていないのが違いの原因だということが判明した。この展開をどう実装するのかも結構悩んだのだが、結局、割とテキトーな方法で済ますことにした。この実装ではRPNを一度二分木に直して、その後再帰的に通常数式化している。たとえば、1 – (2 + (3 – 4))という式は以下のような木構造で表現される。

  '-'
 /   \
1    '+'
    /   \
   2    '-'
       /   \
      3     4

展開が必要になるのは、’-‘と’/’があるノードのright subtree側にそれぞれ’+-‘および’*/’だけからなる部分木が含まれる場合である。テキトー実装では、木を再帰的になめて、’-‘や’/’が出てきたらその右側部分の必要な演算子ノードを逆転させて「展開」している。たとえば上の木ではrootが’’-‘なので、以下のように変更される。

  '-'
 /   \
1    '-'
    /   \
   2    '+'
       /   \
      3     4

この木を、かっこ付けの処理が必要ないふりをしてnaiveに文字列化すると”1 – 2 – 3 + 4″となり、元の式を正しく展開した形になる。変更後の木構造は、値を計算するための木としてはもはや使えないが、ここではこの構造は文字列化するためにしか使っていないのでそれで問題ない。展開が必要な木をrotationしてそうでない形に「標準化」するというような方法(これなら計算にも使える)も考えたのだが、結構手間がかかりそうだったのでこのようなテキトー方法で済ますことにした。

ところで、このような「展開」が本当に必要なのかという点は議論が必要かもしれない。”(1 + 2) + 3″と”1 + (2 + 3)”、あるいは”(1 * 2) + 3″と”1 * 2 + 3″が「同じ式」だというのは、演算子の優先順位と結合の規則だけから決められるし、違いはかっこの有無だけであるが、”1 – (2 + 3)”が”1 – 2 – 3″と同じだとするためには四則演算の計算のルールも必要になる上に一部演算子の書き換えも必要になる。さらに、引き算の場合はまだいいとして、割り算の場合、”A / (B / C)”と”A / B * C”において、Cが0になる場合に両者を「同じ式」と思っていいかどうかはかなり疑問である。…のだが、他の実装と結果が揃っていないと検証もしにくいのでとりあえず今回はこの規則を採用することにした。

一筋縄でいかなかったもう一つの点は速度。まあアルゴリズムと呼ぶのもおこがましいbrute forceなので、多少時間がかかるのは仕方ないのだが、それでも高々1億個程度の割とシンプルな計算にそんなに時間はかからないだろうと思ったら、深く考えずに最初に書いた実装では90分くらいかかってしまった。

少し調べてみると、時間を食っている部分の大半はRPNの計算で、しかも分数の処理のために使っていたpython標準のfractionsモジュールが足を引っ張っているようだった。いろいろ試行錯誤してみて、どうも約分するために最大公約数を求める処理に時間がかかっているのではないかというのが疑われたので、結局自作の簡易版分数クラスを導入することにした。この簡易版実装では、初期化のときも計算時も一切約分しない。RPN全体の計算が終わった時点で結果が整数かどうかを確かめて、その場合のみ割り算してその値を使うようにしている。これで倍くらい速くなった(Pythonの標準ライブラリの実装も、必要になるまで約分を遅延させるように書き換えればかなり速くなるのではないかと思われる)。

その他の試行錯誤の結果として、割り算を含まない式では整数だけで計算するようにするとか、足し算と掛け算だけの式で途中の値が目的値を超えたらそこで打ち切るとかの姑息なチューニングもしているのだが、全体の性能に対しては大して影響がないようだ。

さらに、RPN計算が主なボトルネックであることと、一つの「雛形」に対して多数の計算をまとめてすること、といった構造的な条件から、並列化がかなり有効だと思われたので、この部分の計算を複数のworkerプロセスに分散させられるように改良した。githubにおいたコードで、”-w process数”オプションを使うと複数workerを使うように指定できる。雛形を求める部分にはほとんど時間がかからないので、ここまでをメインのプロセスで実行し、できた雛形をproducer-consumer型のモデルでworkerプロセスに割り振って計算させるようになっている。

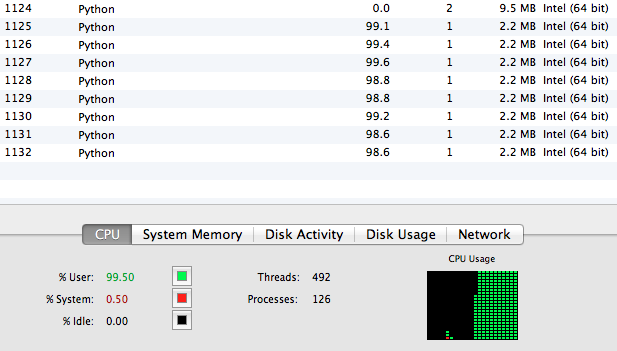
“2010”の場合(どの値でも結局すべての式を計算するので結果は大差ないのだが)で、これを手元のMacBook Pro(Intel Core i7 2.6GHz 4コア 8スレッド)の上で”-w 8″で動かすと約10分で完了する。各雛形の処理が比較的重くてかつ他のworkerから完全に独立しているためだと思われるが、activity monitorで見るとかなり効率よくCPUを使っていることがわかる。

以下のグラフはworker数ごとの所要時間を表したもの。

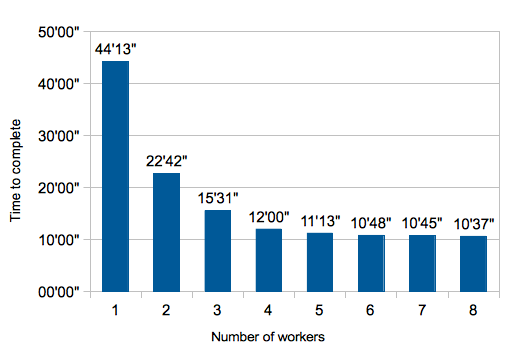
4 workerくらいまではかなりきれいにスケールしている。その先はほぼ頭打ちだが、これはおそらくhyper threadのオーバーヘッドによるものだと思う(それでも8つのworkerを使った方が少しだけ速い)。それぞれのworker間の同期はほとんどないはずなので、本物のコアをもっと積んでいるマシン上で動かせばもっとスケールすると思うのだが、残念ながらいま手元にはこれ以上のスペックのマシンがないので試せない。

最後に: この実装は、特定の値を指定せずに動かすと重複を含まない全ての可能な式(10646016個)とその値を出力する。その内容の一つ一つを検証しているわけではないのだが、個数は上記某先生のblogに記載のものと一致するのでおそらく合っているだろう。今後は、その出力結果(gzipped text, 約80MB72MB)をgrepするのがおそらく最速の「実装」となるだろう。これだと、”2010″の場合の処理は15秒で完了した。